第二卷 希腊 科学精神的起源
今天所谓科学,不是一般的自然知识。它是16、17世纪以来形成的一种特定的意识形态,包含着对事物的特定看法、处理问题的特定方法、知识制造的特定机制;它为人类规定了看待自然、研究自然、征服和改造自然的方式。这个意识形态体系主要是在近代欧洲成长起来的,常常被称作近代科学。
两千多年前希腊人所创造的光辉夺目的文化成就为现代文明奠定了基础。希腊是科学精神的发源地。

拉斐尔的壁画 《雅典学院》,现存于梵蒂冈博物馆。
画面中央神采奕奕走来的是柏拉图(左)和亚里士多德(右),一个左手夹着《蒂迈欧篇》右手指向上方,一个左手持《尼各马可伦理学》右手掌朝下,代表着他们的哲学一个注重理念世界,一个注重现实世界。以他们为中心,展开了激动人心的辩论场面。这两个中心人物的两侧有许多重要的历史人物:左边转身向左扳手指的是苏格拉底,画面中央斜躺在台阶上的半裸着的老人是犬儒学派的哲学家第欧根尼。
台阶下的人物分为左右两组。左边一组中,倚靠在石桌上陷入深思者是赫拉克利特,蹲着在一本大书上专心写字者是毕达哥拉斯,缠着头巾伸头看毕达哥拉斯写字的是阿拉伯学者阿维罗意,阿维罗意左边头戴桂冠就着柱基看书的是伊壁鸠鲁。右边一组的主要人物是欧几里得(一说阿基米德),他正弯腰和四个青年演算几何题。右边身穿黄袍手持天体模型者是托勒密。
第三章 希腊奇迹与科学精神的起源
创造了科学奇迹的古代希腊人生活在包括希腊半岛本土、爱琴海东岸的爱奥尼亚地区、南部的克里特岛以及南意大利地区在内的区域。
希腊奇迹
希腊人热爱自由,不肯屈服于暴君,其民主体制年轻而富有活力;热爱生活,天性乐观,每四年举行一次的奥林匹克竞技会是他们欢乐生活的写照;崇尚理性和智慧,热爱真理,对求知有一种异乎寻常的热忱。
希腊人开启了哲学,也开启了科学,说到底,哲学是科学的纯粹形态。希腊科学是近代科学的真正先驱,几乎在每一领域、每一问题上,希腊人都留下了思考,都是近代科学的老师。
从公元前500年左右开始,希腊人中出现了一大批才智卓越的哲学家和科学家,他们是以后许多学科的鼻祖。在这光辉灿烂的群星中,有最早期的自然哲学家泰勒斯、阿那克西曼德、阿那克西米尼、赫拉克利特、巴门尼德、芝诺、恩培多克勒、阿那克萨哥拉、留基伯、德谟克利特,有人文哲学家普罗泰哥拉、高尔吉亚、苏格拉底,有体系哲学家柏拉图、亚里士多德,有天文学家默冬、欧多克斯、阿克斯塔克、希帕克斯、托勒密,有数学家欧几里得、阿波罗尼、希罗、刁番都,有物理学家阿基米德,有医学家希波克拉底、盖伦,有地理学家希西塔斯、埃拉托色尼,有生物学家特奥弗拉斯特。这些天才人物中有许多不只在一个领域做出开创性工作,而是在多个领域均有建树。像亚里士多德,几乎在每一个知识领域都发表了卓越的见解,是一位不折不扣的百科全书式的学者。
不仅在哲学和科学领域,在文学、历史和艺术方面,希腊人同样毫不逊色。
我们照样可以列出一长串天才的名字:诗人荷马、品达、萨福,寓言家伊索;悲剧大师埃斯库罗斯、索福克勒斯、欧里庇得斯;喜剧大师阿里斯托芬;历史学家希罗多德、修昔底德、色诺芬。哲学家柏拉图的《对话》是无与伦比的韵文,哲学家亚里士多德也是文艺理论家。著名的维纳斯雕像是希腊雕刻艺术的写照。
在地中海沿岸这样一个狭小的区域,在周遭都处在无边的黑暗之中的时候,希腊人不仅在科学、哲学和艺术上做出了伟大的成就,而且创造了一种全新的精神,而这种精神恰恰是真正的现代精神。这才是奇迹所在。
光大东方科学遗产
希腊人之所以创造了这么辉煌的文化成就,是因为他们继承和光大了东方两河流域、尼罗河流域的科学遗产,将之发展到了一个更新的高度。
希腊古典文化是爱琴文明的后代。爱琴文明分为两个阶段,先是克里特文明,再是迈锡尼文明。
早在公元前3000年,克里特岛上的居民已完成了由新石器时代向青铜时代的过渡。克里特岛扼地中海之要冲,海上交通极为便利。它与当时文明程度较高的埃及、小亚细亚、腓尼基有过极为密切的商业贸易往来,东方文化对于克里特文明的形成无疑起着重要的作用。考古学家、古文字学家、历史学家对克里特文明的渊源有进一步的推测,从语言、建筑、科技、艺术等方面的内在联系看,克里特岛甚至有可能是埃及人的殖民地。大约在公元前1400年,克诺索斯宫以及克里特岛其他地方突然遭到破坏。这次大灾难以后,克里特文明就逐渐衰落了。而此时,在希腊本土,迈锡尼文化正如日中天、方兴未艾。
迈锡尼文化因其文化遗址在希腊本土的迈锡尼地区被发现而得名。创造迈锡尼文化的阿卡亚人大约在公元前1600年由北部山区进入希腊中部和南部。他们一开始向先进的克里特文化学习,引入先进的技术和工艺。后来,迈锡尼文化超过了克里特文化。公元前1450年至前1400年间迈锡尼人对克诺索斯王宫的占领,标志着迈锡尼文化的胜利。
公元前1125年左右,同属希腊语系的另一支希腊人多利亚人南下摧毁了迈锡尼,结束了迈锡尼文明时代。落后野蛮的多利亚人摧毁了先进的文化,但没有自己的建树,使希腊历史的这一段呈现出空白,史称“黑暗时期”。但由于留下了两部相传为诗人荷马创作的史诗《伊利昂纪》和《奥德修纪》(旧译《伊利亚特》和《奥德塞》),故又称“荷马时期”。
克里特文明时期,爱琴海地区已经相继出现了象形文字和线形文字A。阿卡亚人(迈锡尼人)吸取线形文字A的某些因素,创造了线形文字B。但自多利亚人摧毁迈锡尼文明以后,线形文字B也中断了。在“黑暗时期”的几百年里,希腊地区没有文字。直到公元前9世纪,腓尼基人发明的字母随着腓尼基商人一起传到了希腊各地,这才形成了后人所看到的希腊文字。
腓尼基人改善和传播了以埃及文字为基本依据的字母表,该字母表后来成了希腊字母表的主体,用来书写科学史和哲学史上最伟大的作品。
希腊神话很大程度上受西亚和埃及的影响,从神的名字、神话典故到神的谱系,都可以找到东方的来源。
正如亚里士多德所说,东方人发展科学知识和技术主要是出于实用的目的和宗教的需要,只有希腊人首先试图给出理性的理解,试图超越具体个别的现象,进入一般的认识。这正是希腊思想的特质,也是希腊人对人类文明的独特贡献。
希腊奴隶制与城邦民主制
亚里士多德在《形而上学》第一卷中提出了希腊学术的两个重要特征。一是出自“惊异”,纯粹为着“求知”;二是以“闲暇”为条件。
希腊人发展科学和哲学,不是为了功利和实用的目的,而只是因为对自然现象和社会现象感到困惑和惊奇,为了解除困惑不得不求知。这样为求知而求知,纯粹是出于一种对智慧的热爱。这是希腊学术的第一个特点。
为希腊人提供闲暇的是希腊奴隶制和希腊的城邦民主制。希腊奴隶制保证了贵族和自由民优裕的生活及闲暇。由于手工作业都由奴隶完成,希腊哲学家养成了轻视体力劳动的习惯。他们一般来说不重视亲自动手观察自然现象、亲手制造仪器工具。他们发展出了高度发达的思维技巧,提出了极富天才的自然哲学理论,但在实验科学方面严重不足。这也是希腊科学的一大特点。
希腊思维方式与科学精神的起源
希腊人,首先把自然当作独立于人的东西整体地看待;其次,他们把自然界看成一个有内在规律的、其规律可以为人所把握的对象;再次,他们发展出了复杂精致的数学工具,以把握自然界的规律。 在这三个方面,希腊人都开了科学精神之先河。
希腊科学和哲学是从希腊神话中脱胎而来的,它为后来西方哲学和科学的发展所奠定的基本观念,同样可以在希腊神话中找到根据。与中国神话相比较可以发现,希腊神话有两个突出特征。
第一个特征是,奥林匹斯山上的诸神与人类相似,但不是人,他们像人一样有个性、有情欲、爱争斗,但同人有严格的界限——所有的人都会死,而神却不死。在中国神话中,人神之别非常模糊。许多人中之杰像神农、伏羲、后羿本身即是神。希腊神话表现的是人神同构,而中国神话表现的是人神同一。同构与同一有着根本的差别,中西哲学传统之差别即已在此表露出来。同构意味着首先这是两个东西,其次才是两个东西相似;其区别是根本的。同构是希腊时代独有的。人神之别,反映了对象性思维的原始形式,而人神同构,则导致了希腊的有机自然观念。作为拟人的世界观,在希腊哲学中,事物是由于分有了宇宙机体的灵魂和心灵才变得能动和理智,也就是说,由于分有了某种结构才变得类似。
希腊神话的第二个突出特征是它完备的诸神谱系:任何一个神都有其来龙去脉,在神谱中的地位非常清楚明白。希腊神话这种完备的诸神谱系,实际上是逻辑系统的原始形式。如果把诸神进一步作为自然事物的象征,那么,系统的神谱可以看作是自然之逻辑构造的原始象征。这种完备的神谱,弘扬了秩序、规则的概念,是希腊理性精神的来源之一。
希腊神话这两大特征,人神相异同构和完备的诸神谱系,反映了希腊思想的对象性和逻辑性。这正是自然科学赖以产生的基本前提。
自然界是有别于人的东西,也是有规律、有秩序的,但更重要的是,它的规律和秩序是人可以把握的,因为它是数学的。对数学的重视,是希腊人最为天才的表现,也是留给近代科学最宝贵的财富。
第四章 希腊古典时代的科学
从第一个自然哲学家泰勒斯开始,到马其顿王亚历山大大帝征服全希腊为止的二百多年,是希腊科学的古典时代。可以按时期和区域分为三个阶段:第一阶段是爱奥尼亚阶段,第二阶段是南意大利阶段,第三阶段是雅典阶段。首先是爱琴海东岸的爱奥尼亚地区。在那里,从泰勒斯开始直到阿那克萨哥拉,形成了以唯物主义自然哲学为特色的爱奥尼亚学派。几乎与此同时,在西方的意大利南部,从毕达哥拉斯开始直到恩培多克勒,形成了以数的哲学为主要特色的南意大利学派。后来,这两个学派相继随地区的衰落而衰落,雅典开始成了主要的活动舞台。著名哲学家苏格拉底、柏拉图和亚里士多德便活跃在雅典的学术讲坛上。
1.第一个自然哲学家泰勒斯
西方历史上第一个自然哲学家泰勒斯诞生于地中海东岸爱奥尼亚地区的希腊殖民城邦米利都。他既是第一个哲学家,也是第一个科学家,是西方科学-哲学的开创者。他的学生阿那克西曼德及后者的学生阿那克西米尼也是米利都人,他们形成了西方哲学史上第一个哲学学派——米利都学派。
泰勒斯的生卒年月无法准确查考。如何知道他的生卒年月呢?对于希腊哲学史上前苏格拉底时期的哲学家来说,这个问题具有某种普遍性。哲学史家发明了“鼎盛年”的概念来解决这一问题,即假定某一哲学家在参与某一重大的历史事件时正处于其最成熟的年龄,而且把这一年龄定为40岁。
泰勒斯年轻的时候曾经游历过巴比伦和埃及,从巴比伦人那里学习了先进的天文学理论,从埃及人那里学习了先进的几何学知识。
泰勒斯本人还亲自观察星象。柏拉图在《泰阿泰德篇》中记述了一段故事,说的是泰勒斯夜里专注于观察天空,不小心掉进了井里。这场景被一位女奴看见了,于是她笑话泰勒斯光热衷于天上发生的事情,却连脚底下的事情都没有看见。这个故事具有象征意义。它表明哲学和科学作为一种理论思维在某种意义上是脱离实际的,没有这种对身边俗务的超脱,没有对看似无实际意义的东西的爱好和关注,就没有哲学和理论自然科学。事情发生在西方第一个哲学家和科学家身上,这种象征意义尤为突出。
泰勒斯第一个把埃及的测地术引进希腊,并将之发展成为比较一般性的几何学。如下几何学定理被认为是泰勒斯提出的:
- 圆周被直径等分;
- 等腰三角形的两底角相等
- 两直线相交时,对顶角相等
- 两三角形中两角及其所夹之边相等,则两三角形全等
- 内接半圆的三角形是直角三角形
泰勒斯作为第一个自然哲学家留下了一句名言:“万物源于水。”这句话的意义不能仅从字面上理解,因为表面看来,一切都来源于水并不正确,但有意义的是这种说话方式。首先,它是一个普遍性命题,它追究万物的共同本原。这是哲学思维的开始,也是科学地对待自然界的第一个原则。科学从具体、复杂、多样的现象中找出共同的原理,再从原理出发解释、说明、预言更多的现象。其次,它开创了唯物主义传统,它所找到的本原是物质性的本原,而不是任何精神性的东西。这也是自然科学的伟大传统之一,即力求用自然界本身说明自然界,而不求助于非自然界的事物。
泰勒斯的学生阿那克西曼德提出宇宙是球状的,星辰镶嵌在圆球上,这是希腊球面天文学的开始。但他还没有地球的概念,他认为大地是柱状的,像鼓一样,有两个彼此相反的表面,人就住在其中一个表面上。阿那克西曼德的学生阿那克西米尼改进了这个宇宙模型,认为宇宙是个半球,像毡帽一样罩在大地上面,大地则像一个盘,浮在气上。阿那克西米尼认为万物都由气组成,气的浓密和稀散造成了不同的物体。在他的著作残篇中有这样的说法:为什么人嘴里可以吐出热气也可以吐出冷气呢?因为闭紧嘴唇压缩气就吐出冷气,放松嘴唇呼出热气。阿那克西米尼的万物由气组成的理论具有现代科学的特征,其呼气实验可以称为第一次真正的科学实验。
爱奥尼亚后来还出现过一个重要的哲学家阿那克萨哥拉。这位出生于米利都附近的希腊殖民城邦的年轻人,因爱奥尼亚被波斯人攻陷而逃往雅典。这次逃亡的结果是把米利都的文化带到了雅典。他继承了米利都学派的唯物主义传统,关注自然哲学问题,提出了独特的物质结构理论——种子论。种子论主张任何感性的物质都不可能互相归结,只能由带有它本身特质的更小的种子来解释;万物的种子在宇宙创生时处于混沌状态,在宇宙巨大的旋涡运动中才开始分离。
2.毕达哥拉斯及其学派
毕达哥拉斯是西方历史上著名的数学家和哲学家,以他的名字命名的毕达哥拉斯定理在西方学童皆知。这个定理在我国被称为勾股定理,它说的是任何一个直角三角形的两直角边的平方和等于其斜边的平方。许多民族都很早就发现了“勾三股四弦五”这一特殊的数学关系,但一般关系的发现和证明是毕达哥拉斯最先做出的。200年后欧几里得的《几何原本》中给出了这一证明。
毕达哥拉斯虽然著名,但他的生平却难以讲清楚。这不仅因为像泰勒斯等早期希腊哲学家一样,由于事久年湮,其历史生平变得模糊,而且因为毕达哥拉斯学派是一个秘密宗教团体,其教义秘不外传。
毕达哥拉斯学派的主要贡献在数学方面。希腊时代的数学含义较广,包括算术、几何、天文学和音乐学四大学科。按照毕氏学派的划分,算术研究绝对的不连续量,音乐研究相对的不连续量,几何学研究静止的连续量,天文学研究运动的连续量。在算术中,他们研究了三角形数、四边形数以及多边形数,发现了三角形数和四边形数的求和规律;在几何学中,他们发现并证明了三角形内角之和等于180°,还研究了相似形的性质,发现平面可以用等边三角形、正方形和正六边形填满。
在音乐学研究的基础上,毕达哥拉斯学派提出了“数即万物”的学说。说数即万物当然是荒谬的,但若说事物遵循的规律是数学的,则相当正确。近代科学正是在追寻自然界的数学规律中取得长足进步的,可以说,许多次重大的突破都是由于发现了新的数学规律。
毕氏学派确实认识到是一个$\sqrt{2}$无理数,并且给出了证明。证明用的是归谬法。设$\sqrt{2}$等于a∶b,其中a和b是不可通约的整数,可以得出a^2^=2b^2^,由于a^2^是偶数,a必为偶数,因为任一奇数的平方必为奇数;a和b既不可通约,a又是偶数,b就必然是奇数。又,a既是偶数就可令a=2c,于是a^2^=4c^2^=2b^2^,b^2^=2c^2^,这样b^2^就是一个偶数,同理b也是一个偶数。b既是一个奇数又是一个偶数,这是矛盾的,所以一开始的假设不能成立,即$\sqrt{2}$不能表示成两个不可通约的整数之比。
在天文学领域,毕氏学派奠定了希腊数理天文学的基础。首先,毕达哥拉斯第一次提出了作为一个圆球的地球概念。其次,毕达哥拉斯进一步提出整个宇宙也是一个球体。
毕达哥拉斯学派既提出了地球概念,也提出了天球概念,这种地球-天球的两球宇宙论模式为希腊天文学奠定了基础。在天球转动的基础上,希腊天文学家运用几何学方法,构造与观测相符合的宇宙模型;在宇宙模型基础上,又进一步促进观测的发展,使希腊数理天文学达到了世界古代科学的顶峰。
3.芝诺的运动悖论
继毕达哥拉斯学派之后,公元前5世纪左右,在南意大利的爱利亚出现了一个新的哲学流派,史称爱利亚学派。他们的领袖是巴门尼德,重要的成员包括芝诺。这派哲学主张存在是“一”,而“杂多”的现象界是不真实的。他们主张世界本质上是静止的,运动只是假象。
他们在科学史上本没有特别重要的位置,但是,由于芝诺提出过两组著名的关于运动是假象的论证,因而为科学史家所重视。这个论证虽说看起来很荒谬,但由于它触及科学概念中一些根本性问题,令数学家们为此苦恼了几千年。
芝诺关于运动的悖论一共有四个。
第一个悖论叫作“二分法”。芝诺说,任何一个物体要想由A点运行到B点,必须首先到达AB的中点C,而要想到达C点,又必须首先到达AC的中点D,要想到达D点,则必须到达AD的中点,等等。这个二分过程可以无限地进行下去,这样,该物体就不可能离开A点运动哪怕一丁点。这个过程可以表示如下:
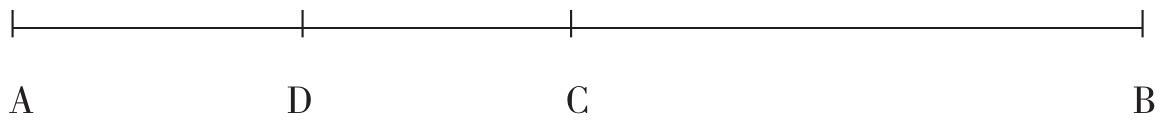
“二分法”还有一种说法:任何物体要想由A点运行到B点必先到达中点C,到了C点之后,又必须到达CB的中点D,到了D之后,又必须到达DB的中点,这样的中点有无限多个,所以,该物体无论如何到不了终点B。
第二个悖论叫作“阿喀琉斯”(又译阿基里斯)
阿喀琉斯是希腊传说中的善跑者,是特洛伊战争中的英雄。芝诺现在论证他追不上乌龟。阿喀琉斯若想追上乌龟,首先必须到达乌龟开始跑的位置,因为乌龟起跑时在阿喀琉斯的前面,有一定的距离。这个要求是合理的,但当快腿阿喀琉斯到达乌龟开始跑的位置时,乌龟已经跑到前面去了。要知道,乌龟虽然跑得慢,但它毕竟在跑。好了,等阿喀琉斯到达乌龟起跑的位置时,他若想追上乌龟又面临同样的问题:他必须先跑到乌龟此刻的位置才能追上乌龟,但等他跑到了,完全同样的问题又摆在他面前。这样的问题可以无限地出现。虽然阿喀琉斯跑得快,他也只能一步一步逼近乌龟,却永远追不上它。乌龟总是在他前头,在他与乌龟之间总有一段距离需要跑,虽然这个距离越来越短,可“总有”。
第三个悖论叫作“飞矢不动”。芝诺说,任何一个东西老待在一个地方那不叫运动,可是飞动着的箭在任何一个时刻不都是待在一个地方吗?既然飞矢在任何一个时刻都待在一个地方,那我们就可以说飞矢不动,因为运动是地方的变动,而在任何一个时刻飞矢的位置并不发生变化,所以任一时刻的飞矢是不动的。既然任一时刻的飞矢不动,那飞矢当然就是不动的。
第四个悖论叫作“运动场”。说的是运动场上三列物体的相对运动所造成的谬误。假设有A、B、C三列物体按如下方式排列:

又假定每一时间单元B和C相对于A运动一个空间单元,但方向相反。于是,在一个时间单元之后三列物体排列如下:

两个时间单元之后排列如下:
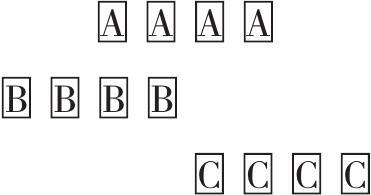
问题出现在,经过一个时间单元后,B与C相互之间有了两个空间单元的移动,经过两个时间单元后,B与C有了四个空间单元的移动。若想B与C只有一个空间单元的移动,那么对应的是半个时间单元,B相对于A移动一个空间单元需要一个时间单元,而相对于C移动一个空间单元却需要半个时间单元,这表明一个时间单元等于半个时间单元。
芝诺的这四个悖论可分为两组。头两个是第一组,假定时间空间是连续的,后两个是第二组,假定时间空间是间断的。每组的第一个悖论表明孤立物体的运动是不可能的,第二个表明两个物体的相对运动是不可能的。芝诺意在表明,无论时空是连续的还是间断的,运动都不可能,都会出现荒谬的事情。
芝诺悖论涉及对时间、空间、无限、运动的看法,它至今还在困扰着哲学家和数学家,这个难题对数学的发展有着重要的积极意义。
4.原子论思想
自然界的现象和事物是复杂多样的,将“多”统一成“一”是不大容易的。特别是在现象的层次上,更是不能服人。由于“多”与“一”的矛盾不能解决,科学思想的概念基础不能牢固建立,科学的大发展就不可能。
原子论者留基伯、德谟克利特是爱奥尼亚人。前者生于米利都,后者生于希腊北部的阿布德拉。他们提出了科学思想史上极为重要的原子论。原子论主张,世界是统一的,自然现象可以得到统一的解释,但统一不是在宏观的层次上进行的,不是将一些自然物归结为另一些自然物,而是将宏观的东西归结为微观的东西。这些微观的东西就是原子。
把一个物体一分为二,它变得更小,但仍然是一个物体,还可以被一分为二。这个过程是否可以无限地进行下去呢?原子论者说,不能。分割过程进行到最后,必然会有一个极限,这个极限就是原子。所谓原子,在希腊文中原意就是不可再分割的东西。原子太小,我们看不见,但世界上的万事万物都是由原子构成的,世界的共同基础是原子。
为什么世界上各种事物会彼此不一样呢?原子论回答说,这是因为组成它们的原子在形状、大小、数量上不一样。这个回答看似平常,但非同一般。我们知道,世界上丰富多彩的事物之所以难于统一,原因在于,它们看起来彼此有质的区别。原子论把这些质的区别还原成量的差异,就使统一的自然界可以用数的科学来描述。
原子论在希腊时代还只是思辨的产物,主要是一种哲学理论,不是科学理论。原子论者留基伯和德谟克利特本人并不是科学家。但是作为一种杰出的科学思想,原子论有其重要的历史地位。近代科学重新复兴了原子论,并在实验基础上构造了物质世界的原子结构。今天,“原子”不再是一种哲学的思辨,而是一个物理学概念。物质由分子构成,分子由原子构成,而原子则由原子核和核外电子组成。20世纪,人们对原子核的内部组成又有了新的发现。这一切科学成就都源于2500年前古希腊原子论者的天才构想。
5.医学之父希波克拉底
有人类生活的地方就有医学。希腊文明作为一种高度发达的文明,不仅有医生和医药,而且有成系统的医学体系。创造医学体系最早的要数爱奥尼亚地区柯斯岛上的希波克拉底。以他的名义流传下来的著作集成《希波克拉底全集》[3],共有大约60篇或长或短的文章(不同的辑本篇数不同)。
希波克拉底最大的贡献是将医学从原始巫术中拯救出来,以理性的态度对待生病、治病。他注意从临床实践出发,总结规律,同时也创立了自己的医学理论,即体液理论。人身上有四种体液,即血液、黄胆汁、黑胆汁和黏液,这四种体液的流动维系着人的生命。它们相互调和、平衡,人就健康,如果平衡破坏,人就生病。这种体液理论一直在西方医学中流传,就像中医的阴阳五行说一样,成了西医的理论基础。
希波克拉底不仅以医术高超著称,而且以医德高尚为人称道。在他周围,形成了一个医学学派和医生团体。他首创了著名的希波克拉底誓词,每一个想当医生的人都要以此宣誓。誓词中说,医生要处处为病人着想,要保持自身行为和这一职业的神圣性。
6.智者与希腊数学三大难题
希波战争使爱奥尼亚的希腊殖民城邦相继陷落。爱奥尼亚的文化精英们大都逃到了雅典。这股东学西渐的潮流不久就导致了雅典文化的黄金时代。希波战争的胜利加强了雅典在希腊世界的地位,政治上的优势带来了经济上的繁荣,经济上的繁荣促进了文化的发展。
人们热衷于谈论政治,谈论法律和规则。辩论术盛行,辩论术士也颇受青睐。在这种特殊的条件下,雅典出现了智者学派(Sophist,中文也译作“巧辩学派”或“诡辩学派”)。这是一群靠卖弄口舌谋生的人。
智者在巧妙、娴熟地运用概念的过程中,促进了逻辑思维的发展。他们之中有许多是著名的几何学家,希腊数学三大难题就是他们提出来的。这三大难题是:
(1)化圆为方,或说,求圆面积。
(2)2倍立方,或说,求一立方体之边,使其体积等于已知边长的立方体的2倍。
(3)三等分任意角。
这三个题目看起来并不困难,为什么会成为希腊数学三大难题呢?实际上,所谓的难题是相对于一定条件来说的,离开条件限制难题就不一定成为难题。对这三个问题,希腊数学家要求只运用直尺和圆规两个工具来解决,这正是难点之所在。
为什么希腊数学家那么严格限制尺规做图呢?一般解释是,希腊人要求逻辑简单明了。直线和圆周是最基本的几何图形,把所有的几何图形化成这两种基本几何图形的组合,是希腊几何学家的理想。
对做图的重视是希腊几何学的一大特色。一个图形必须构造出来,否则就不能成为几何研究的对象。
7.默冬周期的发现
雅典最著名的天文学家是默冬,他继阿那克萨哥拉之后从事天文观测。公元前432年的奥林匹克竞技会上,默冬宣布了他的发现,即19个太阳年与235个朔望月的日数相等。这个周期在我国被称为章,所以默冬周期也常译成默冬章。有了这个周期,就可以确定阴阳历中的置闰规则。235个朔望月的总日数是6940,19年中必有12年是平年,7年是闰年。19年7闰的置闰法在我国被称为章法,它的发现标志着希腊天文观测已达到很高的水平。
8.柏拉图学园:不懂数学者不得入内
雅典学术在柏拉图这里走向系统化。
::: tip 柏拉图
柏拉图出生于雅典的名门世家,他的母亲是梭伦的后裔,父系则可以追溯到古雅典王卡德鲁斯。在这样一个高贵的家庭里,柏拉图从小就受到了当时的人可能受到的最好的教育。年轻的柏拉图立志从事政治,他参加过伯罗奔尼撒战争,表现得十分勇敢。他是苏格拉底最好的学生。传说在他成为苏格拉底学生的头天晚上,苏格拉底梦见一只天鹅来到膝上,很快羽翼丰满,唱着动听的歌儿飞走了。这个传说生动地反映了苏格拉底与柏拉图之间的亲密关系。柏拉图留下的众多对话,大都是以苏格拉底为主要角色。这位可亲可敬的老师却因“败坏青年”等罪状被雅典的民主体制判处死刑。这件事对柏拉图影响很大,他从此决定不再参加政治活动,因为政治太丑恶、太肮脏了。
苏格拉底死后,柏拉图离开了雅典,周游世界。他先到了埃及,后来又到了南意大利,在那里认真研究了毕达哥拉斯学派的理论。柏拉图在外游历十年后,约于公元前387年回到了雅典。
:::
雅典西北郊有一座以英雄阿卡德米命名的圣城。这里自古就是一个公共体育场,柏拉图家族在附近有一座别墅。正当盛年的柏拉图决定在此开设学园,招生讲学。学园的主要目的是促进哲学的发展,但是为了进入哲学,还需要学习许多预备课程,这些课程包括希腊数学的诸种学科:几何学、天文学、音乐学、算术等。据说,柏拉图叫人在学园的门口立了一块牌子:“不懂数学者不得入内”,表明他对数学十分重视。
在柏拉图的哲学中,有一种神圣和高贵的东西,追求纯粹的理想是他的一大特色。他相信,真正实在的不是我们日常所见、所闻的种种常识和感觉。这些东西千变万化,转瞬即逝,是不牢靠的。真正的实在是理念。哲学的目的就是把握理念。理念先于一切感性经验,具有超越的存在,日常世界只是理念世界不完善的摹本。
真正的圆和真正的直线不是我们感觉经验中的圆和直线,而是圆的理念和直线的理念。它们是最容易领悟的理念,因此,通过研究直线和圆这些几何对象更容易进入理念世界。在柏拉图看来,数学是通向理念世界的准备工具,所以在他的学园里,数学研究得到了极大的发展,他的学生中出了不少大数学家。
柏拉图本人对数学的贡献不详,但他对于数学演绎方法的建立和完善肯定起了重要的作用。
在《理想国》中,柏拉图谈到应该重视对立体几何的研究,而且他已经知道正多面体最多只有五种,即正四面体、立方体、正八面体、正十二面体和正二十面体。此外,最重要的发现是圆锥曲线。他们用一个平面去截割一个圆锥面,角度不同会得出不同的曲线:当平面垂直于锥轴时,得到圆;平面稍稍倾斜一点,得到椭圆;平面倾斜到与圆锥的一条母线平行时,得到抛物线;平面与锥轴平行时得到双曲线的一支。
柏拉图的学生中在数学上最有成就的是欧多克斯。欧多克斯在数学上的主要贡献是建立了比例论。越来越多的无理数的发现迫使希腊数学家不得不去研究这些特殊的量,欧多克斯的贡献在于引入了“变量”的概念,把数与量区分开来。在他看来,(整)数是不连续的,而量不一定如此,那些无理数都可由量来代表。数与量的区分方便了几何学的研究,为数学研究不可公度比提供了逻辑依据。但是,人为地将数从几何学中赶出去,使数学家们不再关心线的长度,不再关心算术,而把精力全部投入到几何学中。
欧多克斯更重要的贡献在天文学方面。柏拉图与毕达哥拉斯一样深信,天体是神圣和高贵的,而匀速圆周运动又是一切运动之中最完美、最高贵的一种,所以,天体的运动应该是匀速圆周运动。天上的有些星星恒定不动地做周日运转,而有些星星却不是这样。柏拉图给他的门徒提出了一个任务,即研究行星现在这个样子究竟是由哪些匀速圆周运动叠加而成的。这就是著名的“拯救现象”方法。“拯救”的意思是,行星的现象如此无规则、如此“不体面”,只有找出其所遵循的规则的、高贵的运动方式,才能洗刷这种“不体面”
“拯救现象”是一种科学研究的纲领。我们面对的自然界纷纭复杂、变化万千,如果不把它们纳入一个固定的框架之中,我们便不能很好地把握它们。拯救现象,正是将杂乱的现象归整。希腊时代对人与自然并无严格的区分,对自然现象的“拯救”与对社会秩序的维护确实具有类似的意义。
柏拉图的学园培养了许多优秀的人物,亚里士多德就在这里当过学生。柏拉图在世时,一直亲任学长。他去世之后,由他的外甥斯彪西波担任第二代学长。学园后来虽然在学术上没有什么大的建树,但作为希腊文化的保存者存在了900余年,直到公元529年才被东罗马皇帝查士丁尼勒令关闭。阿卡德米(Akademia)后来成了学院、研究院、学会(academy)的代名词。
9.亚里士多德:百科全书式的学者
柏拉图之后,亚里士多德成为希腊世界最伟大的思想家、哲学家和科学家。
如果说柏拉图是一位综合型的学者,亚里士多德就是一位分科型的学者。他总结了前人已经取得的成就,创造性地提出自己的理论。在几乎每一学术领域,亚里士多德都留下了自己的著作。从第一哲学著作《形而上学》,物理学著作《物理学》《论生灭》《论天》《气象学》《论宇宙》,生物学著作《动物志》《动物的历史》《论灵魂》,到逻辑学著作《范畴篇》《分析篇》,伦理学著作《尼各马可伦理学》《大伦理学》《欧德谟斯伦理学》,以及《政治学》《诗学》《修辞学》等,他的著作几乎遍及每一个学术领域,他是一位名副其实的百科全书式的学者。
亚里士多德的哲学博大精深,自成一体。他不同意柏拉图的理念说,认为事物的本质寓于事物本身之中,是内在的,不是超越的。为了把握世界的真理,必须重视感性经验。就对待自然界的态度而言,这是与柏拉图完全不同的。柏拉图强调理念的超越性,蔑视经验世界,他发展了数学;而亚里士多德重视经验考察,特别在生物学领域取得了卓越的成就。他的哲学目的在于找出事物的本性和原因,因而发展了一套“物理学”,以穷究事物之道理。
在天文学方面,亚里士多德走的还是欧多克斯的路子,即通过天球的组合来解释天体的表观运动。
地上物体,涉及的是物理学的内容。亚里士多德认为,地上物体由土、水、气、火四种元素组成,其运动是直线运动。地上物体都有其天然的处所,而所有的物体都有回到其天然处所的趋势。这一趋势即所谓的天然运动。土和水本质上是重性的,其天然处所在下,因此它们有向下的天然运动;气和火本质上是轻性的,其天然处所在上,因此它们有向上的天然运动。重性越多,下落速度越快,所以重物比轻物下落得快。除了天然运动外,还有受迫运动。受迫运动是推动者加于被推动者的,推动者一旦停止推动,运动就会立刻停止。在自然界中,亚里士多德也发现了等级之分。轻的东西比重的东西高贵,天比地高贵,推动者比被推动者高贵,灵魂比身体高贵。这是亚里士多德物理学中很有特色的东西。
亚里士多德哲学中的四因说对于理解他的生物学成就是有用的。他认为,事物变化的原因有四种,一是质料因,二是形式因,三是动力因,四是目的因。
亚里士多德的生物学著作也许是他的科学工作中最有价值的。在这些著作中,他完全以一个近代生物学家的姿态去观察、实验、总结生物界的现象和规律。
亚里士多德去世后,吕克昂学园由特奥弗拉斯特主持。特氏延续了老师对生物学的研究工作,特别在植物学上做出了重要的贡献。特奥弗拉斯特之后,学园由斯特拉图主持。斯氏主要发展了亚里士多德学说中物理学的方面,把实验方法运用到了物理学领域。为了探讨真空问题,斯特拉图还动手制造了不少仪器。
10.希腊建筑
任何一个古老的文明都可以通过其建筑反映出来。建筑不仅是技术的标志,也是精神风格的象征。从公元前2000年克里特文化时期的米诺斯王宫,到公元前1400年迈锡尼文化时期的卫城,可以依稀看出希腊建筑的宏伟气象。古典时代最重要的建筑都出在雅典。雅典城南面的巴台农神庙(雅典娜处女庙)是雅典建筑最杰出的典范。
巴台农神庙始建于公元前480年,因希波战争受损,再建于公元前447年。它的基座长68米,宽30米,基座上耸立着56根10多米的柱子。高大华丽的列柱是希腊建筑特有的风格。
希腊人喜用柱廊,经长期发展形成了多利亚、爱奥尼亚和科林斯三种风格。到了雅典时期,多利亚式和爱奥尼亚式最为流行。多利亚式建筑庄严朴实,其石柱不设柱基,柱身上细下粗,并刻有凹槽。爱奥尼亚式建筑明快活泼,其石柱下有基座,上有盖盘,柱身细长,凹槽密集。巴台农神庙是典型的多利亚风格建筑。
希腊的柱式建筑别具一格,对日后整个西方建筑的发展有着重要的影响。

第五章 希腊化时期的科学
伯罗奔尼撒战争时期,希腊北部的马其顿王国发展壮大起来。国王腓力二世于公元前356年即位后,注意学习希腊先进的文化,同时富国强兵,扩军备战,不久即建成了希腊世界的一大军事强国。公元前338年,腓力二世击败反马其顿的联军,次年在科林斯召开的泛希腊大会上,确立了马其顿对于希腊各邦的统治地位。公元前336年,腓力二世在宫廷政变中遇刺身亡,20岁的太子亚历山大即位,开始发动对东方的侵略战争。
亚历山大的东征首指波斯帝国,公元前334年大败波斯军队,次年又攻占叙利亚、腓尼基和埃及。公元前331年,亚历山大由埃及出发,与波斯军队再度决战,彻底击败了波斯帝国。亚历山大把巴比伦定为他的新首都,然后继续东征,铁蹄踏到了印度河流域。但因士兵水土不服,大军没再东进。
经过十余年的南征北战,亚历山大建立了一个横跨欧亚非的庞大帝国。这个帝国以东方为中心,但以希腊文化为统治文化。不枉为亚里士多德的学生,军事奇才亚历山大很重视学术事业的发展。在他金戈铁马的生涯中,始终有一批学者跟随。每到一地,地理学家们绘制地图,博物学家们收集标本——据说亚里士多德的生物学研究大大得益于这些珍稀标本。像近代的拿破仑一样,亚历山大也重视科学技术在战争中的作用。据说,由于工程师们的帮助,亚历山大大帝的攻城战水平一度达到了近代的高度。希腊文明就这样随着亚历山大的远征传播到更广大的地区,这些地区的文化也被称为希腊化(hellenistic)文化。
希腊化文化中最耀眼的明珠是亚历山大大帝在埃及建立的城市亚历山大里亚。这个以亚历山大大帝名字命名的城市,产生了古代世界最杰出的科学家和科学成就。本章所谓的希腊化时期的科学指的主要就是亚历山大里亚的科学。
1.亚历山大里亚
亚历山大大帝于公元前323年病逝后,他的帝国分裂成三部分:一部分是安提柯统治下的马其顿,一部分是塞琉古统治下的叙利亚,再就是托勒密统治下的埃及。托勒密将埃及首都设在亚历山大里亚,以政府力量扶助学术事业,造就了亚历山大里亚时代辉煌的科学文化。
亚历山大里亚或称亚历山大城,是随着亚历山大大帝的到来才迅速发展的。马其顿的军事统帅们将希腊文化带到了这里。他们在城里大量建造希腊式建筑。其中最为雄伟的是王宫,据说占整个城市的四分之一或三分之一。亚历山大港口的灯塔被誉为古代世界七大奇观之一。
==托勒密王朝对科学发展的最大贡献是建立了当时世界上最大的国立学术机构“缪塞昂”(Museum)。== 这是一所综合性的教育和研究机构,以传播和发展学术为目的。缪塞昂”原意指祭祀智慧女神缪斯的寺庙,柏拉图的阿卡德米学园和亚里士多德的吕克昂学园里都设有缪塞昂,因此,亚历山大里亚把它的学术机构命名为缪塞昂。这个词后来演化成了英语的“博物馆”。在亚历山大里亚的缪塞昂里,不仅有收藏文物标本的博物馆,而且有动物园、植物园、天文台和实验室。当然,最值得一提的是它的图书馆,藏书达70万卷之多,是当时世界上最大的图书馆。
埃及纸草很多,在亚历山大里亚比在希腊本土更易得到,这是收藏图书的有利条件之一。古代没有印刷术,所谓藏书也就是抄书。托勒密王朝出重金让缪塞昂学院雇用了一大批专门的抄写员,这是使大量藏书成为可能的另一个重要条件。
缪塞昂学院持续了600年之久,但只有最初的200年是科学史上的重要时期。这一时期,科学英才辈出、学术事业繁荣。后来,随着托勒密家族越来越埃及化,他们对希腊学术的兴趣也越来越淡了。据说托勒密七世甚至迫害希腊人。再以后,埃及被罗马人征服,成了罗马的一个省份,希腊的科学遗产逐步丧失殆尽。
2.欧几里得的《几何原本》
在科学史上,没有哪一本书像欧几里得的《几何原本》那样,把卓越的学术水平与广泛的普及性完美结合。它集希腊古典数学之大成,构造了世界数学史上第一个宏伟的演绎系统,对后世数学的发展起了不可估量的推动作用。
::: tip 欧几里得的生平
欧几里得的生平不详。据普罗克罗的记载,他大约于公元前300年应托勒密王的邀请来到亚历山大里亚的缪塞昂学院研究讲学。此前,他在雅典的柏拉图学园受教育,深受柏拉图思想的影响。
关于欧几里得,历史上只留下两则小故事。第一则是普罗克罗记述的,说的是托勒密王请欧几里得为他讲授几何学,讲了半天,托勒密王也没有听懂。于是他问欧几里得有没有更便利的学习方法,欧氏回答说:“在几何学中,没有专为国王设置的捷径。”这句话后来成了传诵千古的治学箴言。第二则故事是斯托拜乌记载的,说的是有一位青年向欧几里得学习几何学,刚学了一个命题,就问欧几里得学了几何学后会有什么用处。欧氏很不满地对仆人说:“给这个学生三个钱币,让他走。他居然想从几何学中捞到实利。”这个故事说明欧几里得很强调几何学的非功利性,也反映了他受到柏拉图很深的影响。
:::
::: tip 几何原本
几何原本》共13篇。第1篇讲直边形,包括全等定理、平行定理、毕达哥拉斯定理、初等做图法等;第2篇讲用几何方法解代数问题,即用几何方法做加减乘除,包括求面积、体积等;第3篇讲圆,讨论了弦、切线、割线、圆心角、圆周角的一些性质;第4篇还是讲圆,主要讲圆的内接和外切图形;第5篇是比例论;第6篇运用已经建立的比例论讨论相似形;第7、8、9、10篇继续讨论数论;第11、12、13篇讲立体几何,其中第12篇主要讨论穷竭法,这是近代微积分思想的早期来源。全部13篇几乎包括了今日初等几何课程中的所有内容。
:::
一般认为,《几何原本》所述内容都属于希腊古典时代,几乎所有的定理都在那时被证明出来了。欧几里得的主要贡献是将它们汇集成一个完美的系统,并且对某些定理给出更简洁的证明。今天我们已无法知道哪些定理是由哪些数学家在什么时候发现的。
欧几里得与阿波罗尼、阿基米德被并称为希腊三大数学家。阿波罗尼大约公元前262年生于小亚细亚西北部的帕加,比欧几里得晚了一个世纪。据说他青年时代到亚历山大里亚跟随欧几里得的学生学习数学,算得上是欧几里得的徒孙,此后一直在亚历山大里亚研究数学。他的主要工作是研究圆锥曲线。其研究领域似乎很专,不像欧几里得的《几何原本》那样涉及广泛,但他之所以能与欧氏齐名,是因为他对圆锥曲线的研究水平极高,空前绝后。单用几何方法来做,今人也不能做得更好。
圆锥曲线,就是用平面截割圆锥体,角度不同将得到不同的曲线。今天的数学家更多采用解析几何的方法处理圆锥曲线问题,将几何问题化为代数问题,既简单又方便,而纯几何方法非常复杂。阿波罗尼在圆锥曲线研究方面的工作,表现出高超的几何思维能力,是古典希腊数学的登峰造极之作,为后世的相关研究奠定了基础。
3.阿里斯塔克:日心说的先驱
哥白尼发现了地球绕太阳转动而不是相反,他使人们从人类中心论的迷梦中惊醒。其实,早在希腊时代就有天文学家提出过日心地动学说,他就是亚历山大里亚的著名天文学家阿里斯塔克。
他的主要主张是,并非日月星辰绕地球转动,而是地球与星辰一起绕太阳转动。恒星的周日运动,其实是地球绕轴自转的结果。这个思想确实是天才的,但过于激进,以至于当时的人们都不相信。
有几个理由导致人们反对阿里斯塔克的观点。第一,它与已经被广泛接受的亚里士多德的物理学理论相矛盾。在亚氏看来,如果地球在运动,那么地球上的东西就都会落在地球的后面,可事实上没有发生这类事情。这个理由很有说服力。这个问题只有在惯性定律被发现之后才会有一个完满的解答。第二,有许多天文学家提出,如果地球在动,那么在地球上观察到的恒星位置在不同的季节应该不一样,可是,我们并没有观测到这种位置的变化。我们不知道阿里斯塔克是如何回答第一个问题的,但据说,他很正确地回答了第二个问题。他说,恒星离我们太远,以至于地球轨道与之相比微不足道,所以,恒星位置的变化不为我们所察觉。
阿里斯塔克另一个重要的天文学成就是测量太阳、月亮与地球的距离以及相对大小。这个工作记载在他的《论日月的大小和距离》一书之中,该书流传到了现在。
阿里斯塔克知道月光是月亮对太阳光的反射,所以,当从地球上看月亮正好半轮亮半轮暗时,太阳、月亮与地球组成了一个直角三角形,月亮处在直角顶点上。从地球上可以测出日地与月地之间的夹角。知道了夹角,就可以知道日地与月地之间的相对距离。阿里斯塔克测得的夹角是87°,因此,他估计日地距离是月地距离的20倍。实际上,夹角应该是89°52′,日地距离是月地距离的346倍。但是,阿里斯塔克的方法是完全正确的。得出了相对距离后,他从地球上所看到的日轮与月轮的大小,推算出太阳与月亮的实际大小。同样,因为没有足够精确的测量数据,其估计误差是很大的,但至少他认识到,太阳是比地球大很多的天体。正因如此,他确实有理由相信不是太阳绕地球转,而是地球绕太阳转,因为,让大的物体绕小的物体转动总不是很自然。
4.古代科学巨匠阿基米德
阿基米德是希腊化时代的科学巨匠。希腊化时期,古希腊人那种纯粹、理想、自由的演绎科学与东方人注重实利、应用的计算型科学进行了卓有成效的融合,实际上为近代科学——既重数学、演绎,又重操作、效益——树立了榜样。阿基米德是希腊化科学的杰出代表。他不仅在数理科学上是一流的天才,而且在工程技术上建树颇多。他也是希腊最富有传奇色彩的科学家。
阿基米德与欧几里得、阿波罗尼并列为希腊三大数学家,甚至有人说他是有史以来最伟大的三位数学家之一(其他两位是牛顿与高斯)。主要数学贡献是求面积和体积的工作。从阿基米德开始,或者说从以阿基米德为代表的亚历山大里亚的数学家开始,算术和代数开始成为一门独立的数学学科。阿基米德发现了一个著名的定理:任一球面的面积是外切圆柱表面积的三分之二,而任一球体的体积也是外切圆柱体积的三分之二。这个定理是从球面积等于大圆面积的4倍这一定理推出来的。
只有直边形的面积以及直边体的体积才可以用算术简单地算出,而曲面的面积和由曲面运动构成的三维体的体积都无法直接算出。欧多克斯发明了穷竭法来解决曲面面积问题,阿基米德更进一步发展了穷竭法。他关于球面面积和球体体积的定理大多是用穷竭法证明的。所谓穷竭法,就是用内接和外切的直边形不断逼近曲边形,这是近代极限概念的直接先驱。运用穷竭法,阿基米德从正6边形开始一直计算到正96边形的周长,得到$3{1\over71} \lt \pi \lt 3{1\over7}$,取小数点后两位得π=3.14。除球面积和球体积的计算外,阿基米德还在抛物面和旋转抛物体的求积方面做了许多杰出的工作。
阿基米德在数学方面的另一著名工作是创造了一套记大数方法。这种方法记载在他流传下来的《恒河沙数》(又译《沙粒计算者》)一书中。
阿基米德在物理学方面的工作主要有两项,一是关于平衡问题的研究,杠杆原理即属于此。二是关于浮力问题的研究,中学物理所学的浮力定律属于此类。在《论平板的平衡》中,阿基米德用数学公理的方式提出了杠杆原理,即杠杆如平衡,则支点两端力(重量)与力臂长度的乘积相等。
阿基米德根据这次在浴盆里的经验进一步总结出了浮力原理:浸在液体中的物体所受到的向上的浮力,其大小等于物体所排开的液体的重量。这个原理定量地给出了浮力的大小,是流体静力学的基本原理之一。
据说,阿基米德在机械工程方面也有许多创造发明。在亚历山大里亚求学期间,他曾发明了一种螺旋提水器,现在仍被称作阿基米德螺旋,直到今天,埃及还有人使用这种器械打水。据说,他还制作了一个利用水力作动力的天象仪,可以模拟天体的运动,演示日食和月食现象。
5.埃拉托色尼测定地球大小
自毕达哥拉斯以来,天球-地球的两球宇宙模型一直是希腊宇宙理论的基础。地球的概念为解释不少近地天文现象如月食提供了可信的依据,而天球的概念则很好地满足了柏拉图学派“拯救现象”的要求。亚历山大里亚有两位著名的学者立足于经验观测和理性判断,进一步丰富了这两个概念。他们中一位是埃拉托色尼,科学地确立了地球的概念,并定量地确定了地球的大小。另一位是希帕克斯,创立了球面几何,为定量地描述天球的运动提供了数学工具。
埃拉托色尼的科学工作包括数学、天文学、地理学和科学史:数学上确定素数的埃拉托色尼筛法是他发明的;在天文学上,他测定了黄道与赤道的交角;在地理学上,他绘制了当时世界上最完整的地图,东到锡兰,西到英伦三岛,北到里海,南到埃塞俄比亚;也许是利用图书馆馆长之便,他还编写了一部希腊科学的编年史,可惜已经失传。
埃拉托色尼最著名的成就是测定地球的大小,其方法完全是几何学的。假定地球真的是一个球体,那么,同一时间在地球上不同的地方,太阳光线与地平面的夹角是不一样的。只要测出这个夹角的差以及两地之间的距离,就可以算出地球的周长。他听人说,在埃及的塞恩,即今日的阿斯旺,夏至这天中午的阳光可以直射入井底,表明这时太阳正好垂直于塞恩的地面。他测出了塞恩到亚历山大里亚的距离,又测出了夏至正午时亚历山大里亚垂直杆的杆长和影长,这样就可以算出地球的周长了。埃拉托色尼算出的数值是25万希腊里,约合4万千米,与地球实际周长相差无几。
6.希帕克斯创立球面三角
希帕克斯是希腊化时期伟大的天文学家。他的卓越贡献是创立了球面三角这个数学工具,使希腊天文学由定性的几何模型变成定量的数学描述,使天文观测有效地进入宇宙模型之中。
自欧多克斯发明同心球模型用以“拯救”天文现象以来,通过球的组合再现行星的运动,已成为希腊数理天文学的基本方法。但传统的方法存在两个问题:首先人们还不知道如何在球面上准确表示行星的位置变化;其次,传统的同心球模型不能解释行星亮度的变化。希帕克斯解决了这两个重要的问题。
通过创立球面三角,希帕克斯解决了第一个问题。根据相似三角形对应边成比例原理,以任一锐角为一角所组成的任何直角三角形,其对边与斜边之比、对边与邻边之比、邻边与斜边之比是一个常数,所以,这些比是角的函数,与边长无关。人们为方便起见就把这些比分别称作正弦、正切、余弦,是为三角函数。希帕克斯第一次全面运用三角函数,并推出了有关定理。更为重要的是,他制定了一张比较精确的三角函数表,以利于人们在实际运算中使用。把平面三角推广到球面上去,也是希帕克斯的工作,因为他的最终目的在于计算行星的球面运动。
解决第二个问题的方法是抛弃同心球模型,创立本轮-均轮体系。一般人都知道这套体系是托勒密体系,但目前知道的最早的使用者实际上是希帕克斯,而发明者是阿波罗尼。每个行星有一个大天球,它以地球为中心转动,这个天球叫均轮。但行星并不处在均轮上,而是处在另一个小天球之上,这个小天球的中心在均轮上,叫本轮。行星既随本轮转动,又随均轮转动,这样可以模拟出比较复杂的行星运动。此外,希帕克斯还引入了阿波罗尼发明的偏心运动,即行星并不绕地球转动,而是绕地球附近的某一空间点转动。
希帕克斯在爱琴海南部的罗得岛建立了一个观象台,制造了许多观测仪器,并做了大量的观测工作。利用自己的观测资料和巴比伦人的观测数据,希帕克斯编制了一幅星图。星图使用了相当完善的经纬度,记载了1000多颗亮星,而且提出了星等的概念,将所有的恒星划为6级。这是当时最先进的星图。借助这幅星图,希帕克斯发现前人记录的恒星位置与他所发现的不一样,存在一个普遍的移动。这样他就发现了,北天极其实并不固定,而是在做缓慢的圆周运动,周期是26700年。由于存在北天极的移动,春分点也随之沿着黄道向西移动,这就使得太阳每年通过春分点的时间总比回到恒星天同一位置的时间早,也就是说,回归年总是短于恒星年。这就是“岁差”现象。
7.希罗与亚历山大里亚的技术成就
在希腊古典时代,技术是不登大雅之堂的。以柏拉图为突出代表,哲学家们大都不屑于与物质的事情打交道,因为那是奴隶下人们的工作。希腊科学局限于理论构想,与现实世界相距甚远。科学没有发挥它对物质世界的改造作用,也未显示它的力量。如果说有力量的话,那也是在精神方面。在马其顿的将军们开辟的亚历山大里亚,气氛有所改变。科学被要求具有物质力量,潮流鼓励科学与技术结盟,因此,在这一时期,亚历山大里亚出现了不少高超的技术成就。
由于没有著作传世,纯技术的成就大多随岁月的流逝而湮没。从各种历史著作的旁记中可以得知,亚历山大里亚在建筑工程、水路和陆路运输工程、军事工程方面都有很多建树,尤其在机械制造方面,更是有不少杰作问世。
早期的工程师有一位叫克特西布斯,大概活跃于公元前285年至前222年。这位理发师的儿子,对技术发明有浓厚的兴趣,并且开创了亚历山大里亚的工程传统。据历史记载,克特西布斯小时候就利用平衡原理为他当理发师的父亲设计了一个可以自由升降的镜子,还发明了压力泵用来压缩空气。利用压缩空气作为动力,他制造了一种弹弓和风琴。克特西布斯最为著名的成就是改进了埃及的水钟。
亚历山大里亚的工程传统在希罗那里达到了高峰。他大概是公元1世纪的人。这个时期,埃及已成为罗马的一个省份,从社会历史分期上讲已进入罗马时代,但是希腊的文明或希腊化的文明并未灭绝,它仍然在沿着自己的轨道发展。许多希腊籍的以及在希腊化文明区接受教育的科学家依然属于希腊文化,而不属于罗马文化,希罗以及本章下面要讲的托勒密、盖伦、刁番都等人都是如此。
希罗有不少科学著作通过阿拉伯文流传下来。他的数学著作有《测量术》《几何学》,据说还有对《几何原本》的注释。这些著作主要从应用方面重新整理前人的数学工作。他的开创性工作在工程技术方面。他的《机械术》中记载了许多机械发明,包括杠杆、滑轮、轮子、斜面、尖劈等机械工具的组合使用。这些东西本质上都是杠杆原理的实际运用。在他的《气体论》中,他指出空气也是一种物质,因为水不能进入充满了空气的容器。他还进一步认识到空气是可以压缩的。在利用空气动力方面,希罗制造了一个很著名的装置,即蒸汽机。这是一个带有两段弯管的空心球体,等球中的水被烧沸之后,蒸汽通过弯管向外喷,产生一个反冲力使球体转动。
8.希腊天文学的集大成者托勒密
近代人最为熟悉的古代天文学家是托勒密。如同欧几里得总结希腊古典时代的数学而写出著名的《几何原本》一样,托勒密系统总结了希腊天文学的优秀成果,写出了流传千古的《天文学大成》。这部13卷的著作被阿拉伯人推为“伟大之至”,结果书名就成了《至大论》(Almagest)。
《至大论》共13卷。第1卷和第2卷给出了地心体系的基本构造,并用一系列观测事实论证了这个模型。按照这个模型,地球是球形的,处在宇宙的中心;诸天体镶嵌在各自的天球上,绕地球转动;按照与地球的距离从小到大排列,天球依次是月亮天、水星天、金星天、太阳天、火星天、木星天、土星天和恒星天。前两卷还讨论了描述这个体系所必需的数学工具,如球面几何和球面三角。第3卷讨论太阳的运动以及与之相关的周年长度的计算,第4卷讨论月球的运动,第5卷计算月地距离和日地距离。他运用希帕克斯的视差法进行计算的结果是,月地距离是地球半径的59倍,日地距离是地球半径的1210倍。这个结果与实际相比,前者比较准确,后者则相差很大。第6卷讨论日食和月食的计算方法,第7卷和第8卷讨论恒星和岁差现象,给出了比希帕克斯星图更详细的星图,而且将恒星按亮度分为6等。从第9卷开始到第13卷,分别讨论了5大行星的运动,本轮和均轮的组合主要在这里得到运用。
托勒密还写过8卷本的《地理学入门》。这本书记述了罗马军团征服世界各地的情况,还依照这些情况画出了更新的世界地图。书中显示托勒密已经知道马来半岛和中国。他也计算了地球的大小,但比埃拉托色尼比较准确的计算结果小了许多。
9.希腊医学的集大成者盖伦
盖伦的主要贡献是系统总结了希腊医学自希波克拉底以来的成就,创立了自成体系的医学理论。他的理论基于自己大量的解剖实践和临床经验,对人体结构和器官的功能有比较正确的描述和说明。
盖伦的生理学把肝脏、心脏和大脑作为人体的主要器官。他认识到肝脏的功能是造血,造血的过程中注入自然的精气。这些血液大部分通过静脉在人的全身做潮汐运动,但有一小部分到了心脏。在心脏中,血液再次被注以生命精气。生命精气通过动脉送往全身,给全身以活力。大脑则将心脏生成的生命精气转变为动物精气,从而支配着肌肉的活动,也使人有表象、记忆和思维的能力。盖伦认识到动脉的功能是输送血液,而不只是输送精气,但他相信这些血液会流到全身各个部位并被吸收。
盖伦的病理学主要继承了传统的四体液说。体液平衡则人体健康,平衡破坏则生病,因此治病主要靠调节各种体液的平衡,排除过剩的和腐败的体液。
盖伦的著作包括医学理论与实践的各个领域,很长时间以来一直被人们所遵从。在欧洲,一千多年来他都是医学上的绝对权威。他确实为西方医学做出了杰出的贡献,因为正是他奠定了西方医学的基础。
10.代数学的创始人刁番都
希腊数学几乎可以等同于希腊几何学,因为希腊数学家几乎都在几何学领域工作。直到希腊化时代的晚期,希腊文明的光辉将要耗尽的时候,才出现了一位伟大的代数学家,他就是刁番都。
刁番都6卷本的《算术》(Arithmetica)原书留传到了现在。书中收集了189个代数问题。与巴比伦时期纯应用性的算术解题不同,刁番都在第1卷中先给出了有关的定义和代数符号说明,依稀有希腊的演绎风格。特别有意义的是,他首先提出了三次以上的高次幂的表示法。这件事在希腊数学史上是划时代的,因为三次以上的高次幂没有几何意义,从前的希腊数学家根本不会考虑它们。这表明从刁番都开始,代数学作为一门独立的学科出现了。
《算术》中的问题除第1卷外大多是不定方程问题,主要是二次和三次方程,例如将一个平方数分为两个平方数之和。对这类问题,刁番都并未给出一个一般的解法,但他确实是最早如此大量地研究不定方程问题。今天人们都把整系数的不定方程称作“刁番都方程”,以表示对他的纪念。刁番都的工作以及亚历山大里亚时期其他数学家在算术和代数方面的工作,都与希腊几何学的研究风格迥然不同。前者注重研究个别问题,后者则注重演绎结构和推理规则。前者在亚历山大里亚时期的兴起,反映了东方科学对希腊化科学的渗透。